Key Word(s): Iterators, Iterables, Trees, B-Trees, Binary search trees

Download Notebook

Lecture 17

Datastructures II

Thursday, October 31st 2019

Last time:

  • Data structures motivation
  • Abstract data types
  • Sequences
  • Linked lists

This time:

From pointers to iterators

One can simply follow the next pointers to the next position in a linked list.

This suggests an abstraction of the position to an iterator.

Such an abstraction allows us to treat arrays and linked lists with an identical interface.

The salient points of this abstraction are:

  • The notion of a next
  • The notion of a first to a last

We already implemented the sequence protocol.

Now we suggest an additional abstraction that is more fundamental than the notion of a sequence: the iterable.

Iterators and Iterables in Python

Just as a sequence is something implementing __getitem__ and __len__, an iterable is something implementing __iter__.

__len__ is not needed and indeed may not make sense.

len(open('fname.txt')) # File iterator has no length

Example 14-1 in Fluent Python: The Sentence sequence and shows how it can be iterated upon.

In [1]:
import reprlib
class Sentence:
    def __init__(self, text): 
        self.text = text
        self.words = text.split()
        
    def __getitem__(self, index):
        return self.words[index] 
    
    def __len__(self):
        #completes sequence protocol, but not needed for iterable
        return len(self.words) 
    
    def __repr__(self):
        return 'Sentence(%s)' % reprlib.repr(self.text)
In [2]:
# Sequence'
s = Sentence("Dogs will save the world.")
print(len(s), "   ", s[3], "   ",  s)

5     the     Sentence('Dogs will save the world.')
In [3]:
print(s)
min(s), max(s)

Sentence('Dogs will save the world.')
Out[3]:
('Dogs', 'world.')
  • list() also acts on iterables
    • e.g. iterators, sequences, containers supporting iteration
In [4]:
list(s)
Out[4]:
['Dogs', 'will', 'save', 'the', 'world.']

To iterate over an object x, Python automatically calls iter(x) (i.e. x.__iter__).

An iterable is something that returns an iterator when iter is called on it.

  1. If __iter__ is defined, it is called to implement an iterator.
  2. If not, __getitem__ is called starting from index 0.
  3. If no __iter__ and no __getitem__, then raise a TypeError.

Any Python sequence is iterable because sequences implement __getitem__. The standard sequences also implement __iter__; for future proofing you should too because (2) might be deprecated in a future version of Python.

We know that for operates on iterables:

In [5]:
for i in s:
    print(i)

Dogs
will
save
the
world.

What's actually going on here?

In [6]:
dir(s)
Out[6]:
['__class__',
 '__delattr__',
 '__dict__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__getitem__',
 '__gt__',
 '__hash__',
 '__init__',
 '__init_subclass__',
 '__le__',
 '__len__',
 '__lt__',
 '__module__',
 '__ne__',
 '__new__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__setattr__',
 '__sizeof__',
 '__str__',
 '__subclasshook__',
 '__weakref__',
 'text',
 'words']
In [7]:
dir(iter(s))
Out[7]:
['__class__',
 '__delattr__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__gt__',
 '__hash__',
 '__init__',
 '__init_subclass__',
 '__iter__',
 '__le__',
 '__length_hint__',
 '__lt__',
 '__ne__',
 '__new__',
 '__next__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__setattr__',
 '__setstate__',
 '__sizeof__',
 '__str__',
 '__subclasshook__']
In [8]:
# A custom for loop
it = iter(s) # Build an iterator from an iterable
while True:
    try:
        nextval = next(it) # Get the next item in the iterator
        print(nextval)
    except StopIteration:
        del it # Iterator is exhausted.  Release reference and discard.
        break

Dogs
will
save
the
world.
In [9]:
it = iter(s)
print(next(it))
print(next(it))
print(next(it))
print(next(it))
print(next(it))
print(next(it)) # Exhaust iterator!

Dogs
will
save
the
world.

---------------------------------------------------------------------------
StopIteration                             Traceback (most recent call last)
 in 
      5 print(next(it))
      6 print(next(it))
----> 7 print(next(it)) # Exhaust iterator!

StopIteration:

Once an iterator is exhausted, a new iterator must be built from the iterable if we want to go through it again.

We can completely abstract away a sequence in favor of an iterable (i.e. we don't need to support indexing anymore).

Example 14-4 in Fluent Python:

In [10]:
class SentenceIterator: # has __next__ and __iter__
    def __init__(self, words): 
        self.words = words 
        self.index = 0 # Determines the next word to fetch
        
    def __next__(self): 
        try:
            word = self.words[self.index] 
        except IndexError:
            raise StopIteration() 
        self.index += 1
        return word 

    def __iter__(self):
        return self #  Allows iterators to be used where an iterable is expected
In [11]:
class Sentence: # An iterable b/c it has __iter__
    def __init__(self, text): 
        self.text = text
        self.words = text.split()
        
    def __iter__(self):
        return SentenceIterator(self.words) # Returns an instance of the iterator
    
    def __repr__(self):
        return 'Sentence(%s)' % reprlib.repr(self.text)
In [12]:
s2 = Sentence("What is data science?")
In [13]:
for i in s2:
    print(i)

What
is
data
science?
In [14]:
s2it = iter(s2) # Make the iterable an iterator
print(next(s2it), "\n") # Get the next entry

s2it2 = iter(s2) # Reset the iterator
print(next(s2it), "   ", next(s2it2)) # Get the next entry of s2it and s2it2

What 

is     What

What if...?

The Gang of Four (GoF) design patterns book says that iterators must also be iterable.

Why does this make sense?

In [15]:
class BadSentenceIterator: # has __next__ and __iter__
    def __init__(self, words): 
        self.words = words 
        self.index = 0 # Determines the next word to fetch
        
    def __next__(self): 
        try:
            word = self.words[self.index] 
        except IndexError:
            raise StopIteration() 
        self.index += 1
        return word
In [16]:
si = BadSentenceIterator(list('Dogs will save the world.'.split()))
for s in si:
    print(s)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
 in 
      1 si = BadSentenceIterator(list('Dogs will save the world.'.split()))
----> 2 for s in si:
      3     print(s)

TypeError: 'BadSentenceIterator' object is not iterable
In [17]:
class GoodSentenceIterator: # has __next__ and __iter__
    def __init__(self, words): 
        self.words = words 
        self.index = 0 # Determines the next word to fetch
        
    def __next__(self): 
        try:
            word = self.words[self.index] 
        except IndexError:
            raise StopIteration() 
        self.index += 1
        return word
    
    def __iter__(self):
        return self
In [18]:
si = GoodSentenceIterator(list('Dogs will save the world.'.split()))
for s in si:
    print(s)

Dogs
will
save
the
world.

A Warning

While we could have implemented __next__ in Sentence itself, making it an iterator, we will run into the problem of "exhausting an iterator".

The iterator above keeps state in self.index and we must be able to start over by creating a new instance if we want to re-iterate. Thus the __iter__ in the iterable simply returns the SentenceIterator.

"Relationship between iterables and iterators: Python obtains iterators from iterables."

From Fluent Python ("Sentence Take #2: A Classic Iterator"):

A common cause of errors in building iterables and iterators is to confuse the two. To be clear: iterables have an __iter__ method that instantiates a new iterator every time. Iterators implement a __next__ method that returns individual items, and an __iter__ method that returns self.

min() and max() also work even though we no longer satisfy the sequence protocol.

min and max are pairwise comparisons and can be handled via iteration.

The take home message is that in programming with these iterators we don't need either the length or indexing to work to implement many algorithms: we have abstracted these away.

In [19]:
min(s2), max(s2)
Out[19]:
('What', 'science?')

Trees

  • A tree is a hierarchical data structure that has a bunch of items.
  • Each item may have a value.
  • Items may point to other items or not (leaf nodes).
  • Each item is pointed to by exactly one other item with the sole exception of the root item. Nothing points to the root item.

There are many types of trees used to express data structures. For example,

  • Binary Tree
  • B-Tree
  • Heap
  • Multi-way tree

Each of these has many subtypes.

Trees arise everywhere:

  • In parsing of code
  • Evolutionary trees in biology
  • Language origin trees
  • Unix file system
  • HTML tags

Just like with lists, one can consider looking at a tree in two ways: a collection of nodes or a tree with a root and multiple sub-trees.

Today, and in your homework, the focus is on Binary trees.

Once again, one can represent trees using the recursive data structures we used to represent linked lists (from cs61a):

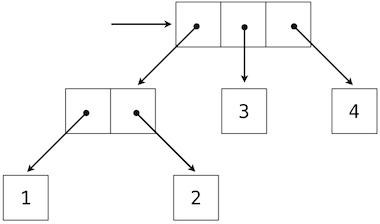
You could also use a tree in which the nodes all themselves have data. This is often used to represent a binary tree.

Some Terminology (Binary Tree)

  • The root node is the only node that has nothing pointing to it.
  • A node can point to other nodes called children.
  • The node doing the pointing is called the parent node.
  • In a binary tree, a given node only points to two other nodes (maximum of two children).
  • If a child node does not contain a value, then it is said to be empty (or null).
  • A node with pointers to two empty values is called a leaf.

Binary Search Trees (BSTs)

These are binary trees with the requirement that all children to the left of a particular node have lower values and all children to the right have higher values.

There are ways of dealing with repeated values (e.g. storing a counter), but we will just use BSTs that do not have repeated values.

A major benefit of BSTs:

  • Time complexity an be $O(\log_{2}(n))$ for a balanced tree where $n$ is the # of items stored in the tree.
In [20]:
import numpy as np
import matplotlib.pyplot as plt
In [21]:
n = np.logspace(1, 25, 100, base=2)
fig, ax = plt.subplots(1,1, figsize=(10,6))
ax.plot(n,n, ls='--', lw=5, label=r'$n$')
ax.plot(n, np.log2(n), lw=5, label=r'$\log_{2}\left(n\right)$')
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel(r'$n$', fontsize=32)
ax.set_ylabel(r'Time Complexity', fontsize=32)
ax.tick_params(axis='both', which='major', labelsize=32)
ax.legend(fontsize=32)
Out[21]:

An algorithm for the deletion of a node is as follows:

  1. If the node to be deleted has no children, then just remove it.
  2. If the node to be deleted has only one child, remove the node and replace it with its child.
  3. If the node to be deleted has two children, replace the node to be deleted with the maximum value in the left subtree. Finally, delete the node with the maximum value in the left-subtree.