CS-109B Advanced Data Science

Lab 6: Recurrent Neural Networks¶

Harvard University
Spring 2019
Lab instructor: Srivatsan Srinivasan
Instructors: Pavlos Protopapas and Mark Glickman
Authors: Srivatsan Srinivasan, Pavlos Protopapas

In [ ]:

# RUN THIS CELL TO PROPERLY HIGHLIGHT THE EXERCISES
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2019-CS109B/master/content/styles/cs109.css").text
HTML(styles)

Learning Goals¶

In this lab we will look at Recurrent Neural Networks (RNNs), LSTMs and their building blocks.

By the end of this lab, you should:

know how to put together the building blocks used in RNNs and its variants (GRU, LSTM) in keras with an example.
have a good undertanding on how sequences - any dataset that has some temporal semantics (time series, natural language, images etc.) fit into and benefit from a recurrent architecture
be familiar with preprocessing text, dynamic embeddings
be familiar with gradient issues on RNNs processing longer sentence lengths
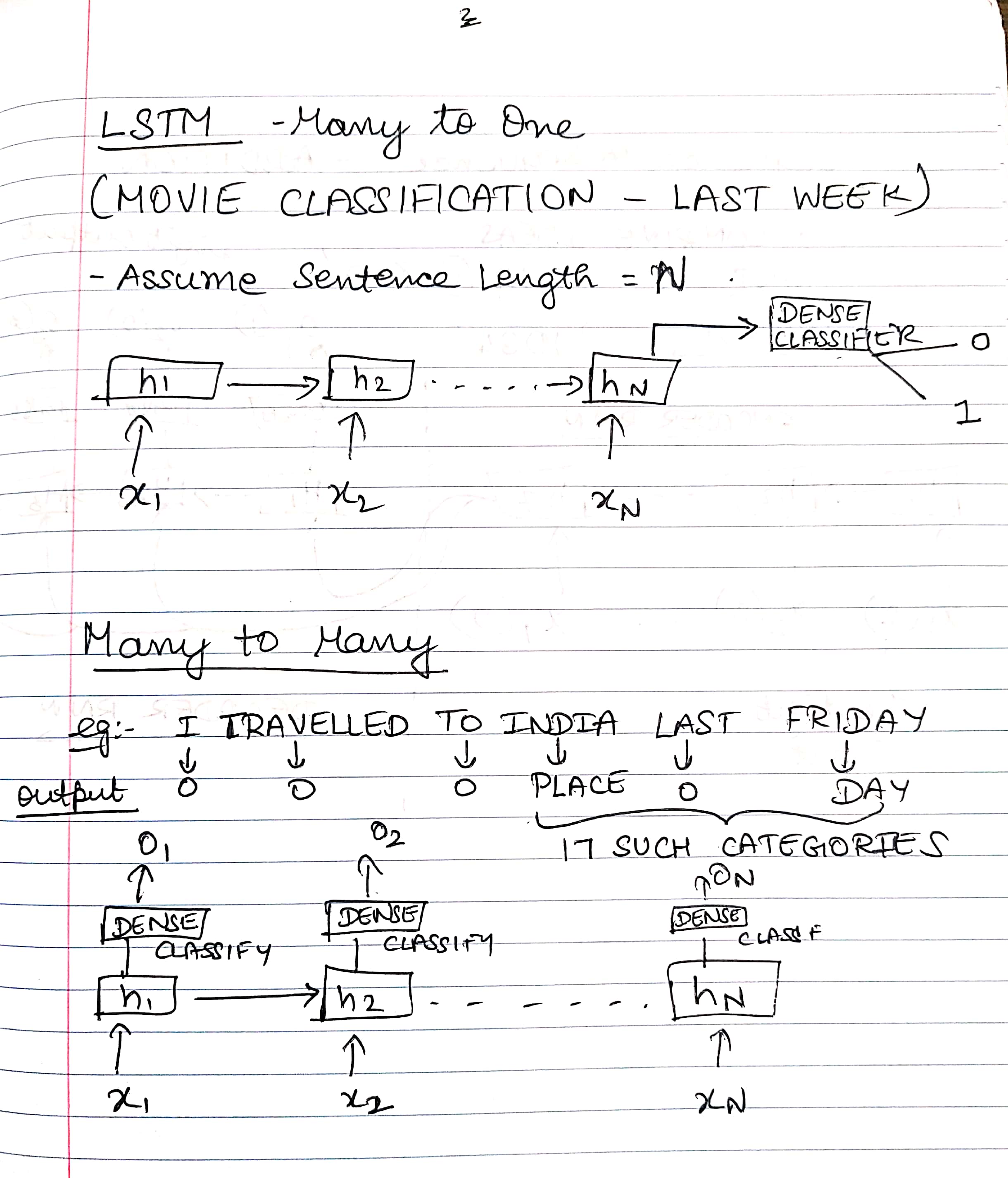
understand different kinds of LSTM architectures - classifier, sequence to sequence models and their far-reaching applications

1. IMDB Review Classification Battlefield - Contestants : Feedforward, CNN, RNN, LSTM¶

In this task, we are going to do sentiment classification on a movie review dataset. We are going to build a feedforward net, a convolutional neural net, a recurrent net and combine one or more of them to understand performance of each of them. A sentence can be thought of as a sequence of words which have semantic connections across time. By semantic connection, we mean that the words that occur earlier in the sentence influence the sentence's structure and meaning in the latter part of the sentence. There are also semantic connections backwards in a sentence, in an ideal case (in which we use RNNs from both directions and combine their outputs). But for the purpose of this tutorial, we are going to restrict ourselves to only uni-directional RNNs.

In [ ]:

import numpy
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM, SimpleRNN
from keras.layers.embeddings import Embedding
from keras.layers import Flatten
from keras.preprocessing import sequence
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
from keras.layers.embeddings import Embedding
import numpy as np
# fix random seed for reproducibility
numpy.random.seed(1)

In [ ]:

# We want to have a finite vocabulary to make sure that our word matrices are not arbitrarily small
vocabulary_size = 10000

#We also want to have a finite length of reviews and not have to process really long sentences.
max_review_length = 500

TOKENIZATION¶

For practical data science applications, we need to convert text into tokens since the machine understands only numbers and not really English words like humans can. As a simple example of tokenization, we can see a small example.

Assume we have 5 sentences. This is how we tokenize them into numbers once we create a dictionary.

i have books - [1, 4, 7]
interesting books are useful [10,2,9,8]
i have computers [1,4,6]
computers are interesting and useful [6,9,11,10,8]
books and computers are both valuable. [2,10,2,9,13,12]
Bye Bye [7,7]

Create tokens for vocabulary based on frequency of occurrence. Hence, we assign the following tokens

I-1, books-2, computers-3, have-4, are-5, computers-6,bye-7, useful-8, are-9, and-10,interesting-11, valuable-12, both-13

Thankfully, in our dataset it is internally handled and each sentence is represented in such tokenized form.

Load data¶

In [ ]:

(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=vocabulary_size)

print('Number of reviews', len(X_train))
print('Length of first and fifth review before padding', len(X_train[0]) ,len(X_train[4]))
print('First review', X_train[0])
print('First label', y_train[0])

Preprocess data¶

Pad sequences in order to ensure that all inputs have same sentence length and dimensions.

In [ ]:

X_train = sequence.pad_sequences(X_train, maxlen=max_review_length)
X_test = sequence.pad_sequences(X_test, maxlen=max_review_length)
print('Length of first and fifth review after padding', len(X_train[0]) ,len(X_train[4]))

MODEL 1(a) : FEEDFORWARD NETWORKS WITHOUT EMBEDDINGS¶

Let us build a single layer feedforward net with 250 nodes. Each input would be a 500-dim vector of tokens since we padded all our sequences to size 500.

EXERCISE : Calculate the number of parameters involved in this network and implement a feedforward net to do classification without looking at cells below.

In [ ]:

model = Sequential()

model.add(Dense(250, activation='relu',input_dim=max_review_length))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())


model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

Discussion : Why was the performance bad ? What was wrong with tokenization ?¶

MODEL 1(b) : FEEDFORWARD NETWORKS WITH EMBEDDINGS¶

What is an embedding layer ?¶

An embedding is a linear projection from one vector space to another. We usually use embeddings to project the one-hot encodings of words on to a lower-dimensional continuous space so that the input surface is dense and possibly smooth. According to the model, an embedding layer is just a transformation from $\mathbb{R}^{inp}$ to $\mathbb{R}^{emb}$

In [ ]:

embedding_dim = 100

In [ ]:

model = Sequential()

model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
#inputs will be converted from batch_size * sentence_length to batch_size*sentence_length*embedding _dim
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

In [ ]:

# Fit the model
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

MODEL 2 : CONVOLUTIONAL NEURAL NETWORKS¶

Text can be thought of as 1-dimensional sequence and we can apply 1-D Convolutions over a set of words. Let us walk through convolutions on text data with this blog.

http://debajyotidatta.github.io/nlp/deep/learning/word-embeddings/2016/11/27/Understanding-Convolutions-In-Text/

Fit a 1D convolution with 200 filters, kernel size 3 followed by a feedforward layer of 250 nodes and ReLU, sigmoid activations as appropriate.

In [ ]:

# create the model
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=200, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

MODEL 3 : SIMPLE RNN¶

Two of the best blogs that help understand the workings of a RNN and LSTM are

Mathematically speaking, a simple RNN does the following. It constructs a set of hidden states using the state variable from the previous timestep and the input at current time. Mathematically, a simpleRNN can be defined by the following relation.

$h_t = \sigma(W([h_{t-1},x_{t}])+b)$

If we extend this recurrence relation to the length of sequences we have in hand, we have our RNN network constructed.

In [ ]:

model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(SimpleRNN(100))

model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

RNNs and vanishing/exploding gradients¶

Let us use sigmoid activations as example. Derivative of a sigmoid can be written as

$\sigma'(x) = \sigma(x) \cdot \sigma(1-x)$.

Remember RNN is a "really deep" feedforward network (when unrolled in time). Hence, backpropagation happens from $h_t$ all the way to $h_1$. Also realize that sigmoid gradients are multiplicatively dependent on the value of sigmoid. Hence, if the non-activated output of any layer $h_l$ is < 0, then $\sigma$ tends to 0, effectively "vanishing" gradient. Any layer that the current layer backprops to $H_{1:L-1}$ do not learn anything useful out of the gradients.

LSTMs and GRU¶

LSTM and GRU are two sophisticated implementations of RNN which essentially are built on what we call as gates. A gate is a probability number between 0 and 1. For instance, LSTM is built on these state updates

Note : L is just a linear transformation L(x) = W*x + b.

$f_t = \sigma(L([h_{t-1},x_t))$

$i_t = \sigma(L([h_{t-1},x_t))$

$o_t = \sigma(L([h_{t-1},x_t))$

$\hat{C}_t = \tanh(L([h_{t-1},x_t))$

$C_t = f_t * C_{t-1}+i_t*\hat{C}_t$ (Using the forget gate, the neural network can learn to control how much information it has to retain or forget)

$h_t = o_t * \tanh(c_t)$

MODEL 4 : LSTM¶

In the next step, we will implement a LSTM model to do classification. Use the same architecture as before. Try experimenting with increasing the number of nodes, stacking multiple layers, applyong dropouts etc. Check the number of parameters that this model entails.

In [ ]:

model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

MODEL 5 : CNN + LSTM¶

CNNs are good at learning spatial features and sentences can be thought of as 1-D spatial vectors (dimension being connotated by the sequence ordering among the words in the sentence.). We apply a LSTM over the features learned by the CNN (after a maxpooling layer). This leverages the power of CNNs and LSTMs combined. We expect the CNN to be able to pick out invariant features across the 1-D spatial structure(i.e. sentence) that characterize good and bad sentiment. This learned spatial features may then be learned as sequences by an LSTM layer followed by a feedforward for classification.

In [ ]:

model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=32, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())

model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

CONCLUSION¶

We saw the power of sequence models and how they are useful in text classification. They give a solid performance, low memory footprint (thanks to shared parameters) and are able to understand and leverage the temporally connected information contained in the inputs. There is still an open debate about the performance vs memory benefits of CNNs vs RNNs in the research community.

2. 231+432 = 665.... It's not ? Let's ask our LSTM¶

In this exercise, we are going to teach addition to our model. Given two numbers (<999), the model outputs their sum (<9999). The input is provided as a string '231+432' and the model will provide its output as ' 663' (Here the empty space is the padding character). We are not going to use any external dataset and are going to construct our own dataset for this exercise.

The exercise we attempt to do effectively "translates" a sequence of characters '231+432' to another sequence of characters ' 663' and hence, this class of models are called sequence-to-sequence models. Such architectures have profound applications in several real-life tasks such as machine translation, summarization, image captioning etc.

In [ ]:

from __future__ import print_function
from keras.models import Sequential
from keras import layers
from keras.layers import Dense, RepeatVector, TimeDistributed
import numpy as np
from six.moves import range

The less interesting data generation and preprocessing¶

In [ ]:

class CharacterTable(object):
    def __init__(self, chars):        
        self.chars = sorted(set(chars))
        self.char_indices = dict((c, i) for i, c in enumerate(self.chars))
        self.indices_char = dict((i, c) for i, c in enumerate(self.chars))

    #One-hot encodes
    def encode(self, C, num_rows):        
        x = np.zeros((num_rows, len(self.chars)))
        for i, c in enumerate(C):
            x[i, self.char_indices[c]] = 1
        return x
    
    #Decodes a one-hot encoding
    def decode(self, x, calc_argmax=True):        
        if calc_argmax:
            x = x.argmax(axis=-1)
        return ''.join(self.indices_char[x] for x in x)

In [ ]:

TRAINING_SIZE = 50000
DIGITS = 3
MAXOUTPUTLEN = DIGITS + 1
MAXLEN = DIGITS + 1 + DIGITS

chars = '0123456789+ '
ctable = CharacterTable(chars)

In [ ]:

def return_random_digit():
  return np.random.choice(list('0123456789'))  
  
def generate_number():
  num_digits = np.random.randint(1, DIGITS + 1)  
  return int(''.join( return_random_digit()
                      for i in range(num_digits)))

def data_generate(num_examples):
  questions = []
  expected = []
  seen = set()
  print('Generating data...')
  while len(questions) < TRAINING_SIZE:      
      a, b = generate_number(), generate_number()  
      #Remove already seen elements
      key = tuple(sorted((a, b)))
      if key in seen:
          continue
      seen.add(key)
      # Pad the data with spaces such that it is always MAXLEN.
      q = '{}+{}'.format(a, b)
      query = q + ' ' * (MAXLEN - len(q))
      ans = str(a + b)
      # Answers can be of maximum size DIGITS + 1.
      ans += ' ' * (MAXOUTPUTLEN - len(ans))
      questions.append(query)
      expected.append(ans)
  print('Total addition questions:', len(questions))
  return questions, expected


def encode_examples(questions,answers):
  x = np.zeros((len(questions), MAXLEN, len(chars)), dtype=np.bool)
  y = np.zeros((len(questions), DIGITS + 1, len(chars)), dtype=np.bool)
  for i, sentence in enumerate(questions):
      x[i] = ctable.encode(sentence, MAXLEN)
  for i, sentence in enumerate(answers):
      y[i] = ctable.encode(sentence, DIGITS + 1)

  indices = np.arange(len(y))
  np.random.shuffle(indices)
  return x[indices],y[indices]

In [ ]:

q,a = data_generate(TRAINING_SIZE)
x,y = encode_examples(q,a)
split_at = len(x) - len(x) // 10
x_train, x_val, y_train, y_val = x[:split_at], x[split_at:],y[:split_at],y[split_at:]


print('Training Data shape:')
print('X : ', x_train.shape)
print('Y : ', y_train.shape)

print('Sample Question(in encoded form) : ', x_train[0], y_train[0])
print('Sample Question(in decoded form) : ', ctable.decode(x_train[0]),'Sample Output : ', ctable.decode(y_train[0]))

Let's learn two wrapper functions in Keras - TimeDistributed and RepeatVector with some dummy examples.¶

TimeDistributed is a wrapper function call that applies an input operation on all the timesteps of an input data. For instance I have a feedforward network which converts a 10-dim vector to a 5-dim vector, then wrapping this timedistributed layer on that feedforward operation would convert a batch_size * sentence_len * vector_len(=10) to batch_size * sentence_len * output_len(=5)

In [ ]:

model = Sequential()
#Inputs to it will be batch_size*time_steps*input_vector_dim(to Dense) . Output will be batch_size*time_steps* output_vector_dim
#Here dense converts a 5-dim input vector to a 8-dim vector.
model.add(TimeDistributed(Dense(8), input_shape=(3, 5)))
input_array = np.random.randint(10, size=(1,3,5))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)

RepeatVector repeats the vector a specified number of times. Dimension changes from batch_size number of elements to batch_size number of repetitions * number of elements.

In [ ]:

model = Sequential()
#converts from 1*10 to 1 * 6
model.add(Dense(6, input_dim=10))
print(model.output_shape)
#converts from 1*6 to 1*3*6
model.add(RepeatVector(3))
print(model.output_shape) 
input_array = np.random.randint(1000, size=(1, 10))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)
# note: `None` is the batch dimension
print('Input : ', input_array[0])
print('Output : ', output_array[0])

MODEL ARCHITECTURE¶

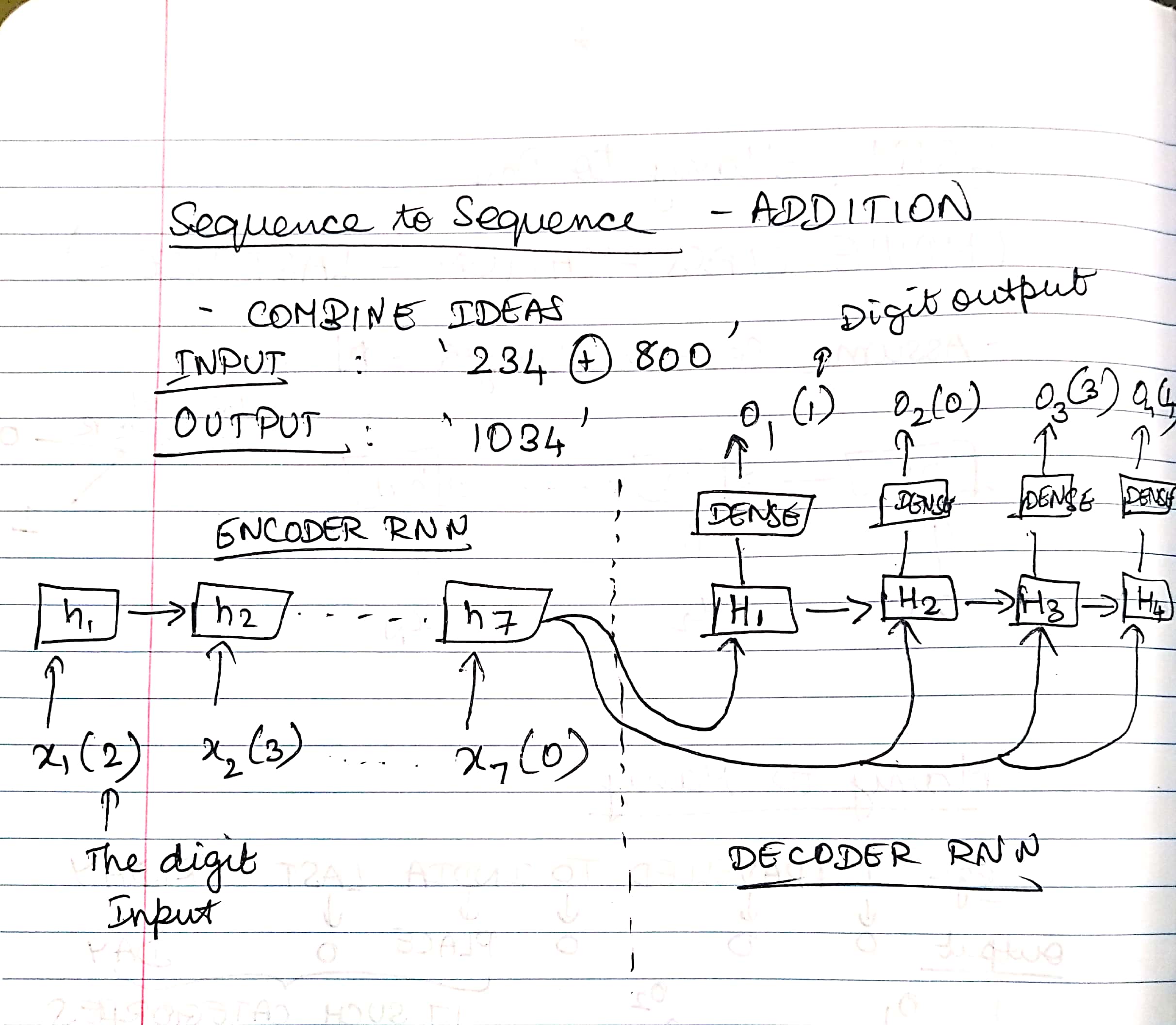
Note : Whenever you are initializing a LSTM in Keras, by the default the option return_sequences = False. This means that at the end of the step the next component will only get to see the final hidden layer's values. On the other hand, if you set return_sequences = True, the LSTM component will return the hidden layer at each time step. It means that the next component should be able to consume inputs in that form.

Think how this statement is relevant in terms of this model architecture and the TimeDistributed module we just learned.

Build an encoder and decoder both single layer 128 nodes and an appropriate dense layer as needed by the model.

In [ ]:

#Hyperaparams
RNN = layers.LSTM
HIDDEN_SIZE = 128
BATCH_SIZE = 128
LAYERS = 1

print('Build model...')
model = Sequential()
#ENCODING
model.add(RNN(HIDDEN_SIZE, input_shape=(MAXLEN, len(chars))))
model.add(RepeatVector(MAXOUTPUTLEN))
#DECODING
for _ in range(LAYERS):    
    model.add(RNN(HIDDEN_SIZE, return_sequences=True))

model.add(TimeDistributed(layers.Dense(len(chars), activation='softmax')))
model.compile(loss='categorical_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])
model.summary()

Let's check how well our model trained.

In [ ]:

for iteration in range(1, 2):
    print()  
    model.fit(x_train, y_train,
              batch_size=BATCH_SIZE,
              epochs=20,
              validation_data=(x_val, y_val))
    # Select 10 samples from the validation set at random so we can visualize
    # errors.
    print('Finished iteration ', iteration)
    numcorrect = 0
    numtotal = 20
    
    for i in range(numtotal):
        ind = np.random.randint(0, len(x_val))
        rowx, rowy = x_val[np.array([ind])], y_val[np.array([ind])]
        preds = model.predict_classes(rowx, verbose=0)
        q = ctable.decode(rowx[0])
        correct = ctable.decode(rowy[0])
        guess = ctable.decode(preds[0], calc_argmax=False)
        print('Question', q, end=' ')
        print('True', correct, end=' ')
        print('Guess', guess, end=' ')
        if guess == correct :
          print('Good job')
          numcorrect += 1
        else:
          print('Fail')
    print('The model scored ', numcorrect*100/numtotal,' % in its test.')

EXERCISE¶

Try changing the hyperparams, use other RNNs, more layers, check if increasing the number of epochs is useful.
Try reversing the data from validation set and check if commutative property of addition is learned by the model. Try printing the hidden layer with two inputs that are commutative and check if the hidden representations it learned are same or similar. Do we expect it to be true ? If so, why ? If not why ? You can access the layer using an index with model.layers and layer.output will give the output of that layer.

Try doing addition in the RNN model the same way we do by hand. Reverse the order of digits and at each time step, input two digits get an output use the hidden layer and input next two digits and so on.(units in the first time step, tens in the second time step etc.)